neural network-白红宇

neural network

阅读量：5256 次

发布时间：2019-06-14

本文共 2881 字，大约阅读时间需要 9 分钟。

some example

当x为binary时

structure

以四层的multi-class classification为例（以01向量列表示分类预测。第i个最接近1则预测为第i个）

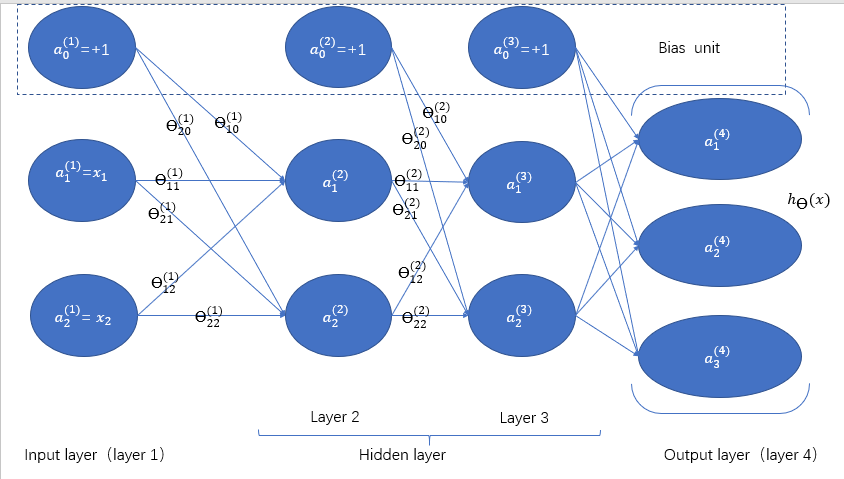$\theta^{(l)}_{ji}$表示第$l$层第$i$个神经元到下一层第$j$个神经元的转移的系数

记$S_l$为第$l$层除了bias unit之外的unit个数

则$\theta^{(l)}$大小为$S_{l+1}\times(S_l + 1)$

$a^{(l+1)}=sigmoid(\theta^{(l)} a^{(l)})$ (别漏了sigmoid)

存储时每层一个列向量这样比较好

cost function

对于multiclass-classification

$h_{\theta}$是指从input到output

\[J(\theta) = -\frac 1 m\sum_{k=1}^K \sum_{i=1}^m \left[ y^{(i)}_k\ln(h_{\theta}(x^{(i)}))_k+(1-y^{(i)}_k)\ln(1-h_{\theta}(x^{(i)}))_k \right] + \frac{\lambda}{2m} \sum_{l=1}^{L-1} \sum_{i=1}^{S_l} \sum_{j=1}^{S_{l+1}} (\theta^{l}_{ji})^2\]

注意$i$不从0开始

这个J是non-convex，有local minimum

gradient (FP & BP)

P = propagation

F = forward

B = backward

先忽略掉regularization的部分

相当于求$-\frac 1 m\sum_{k=1}^K \sum_{i=1}^m y_k^{(i)} ln(a^{(L)}_k) + (1-y_k^{(i)}) ln(1 - a^{(L)}_k)$

根据之前在classification中的推导，我们记得配合sigmoid函数可以把这个复杂的函数求导后变得很简单

因为转移为$z^{(L)}_j = a^{(L-1)}_i \theta^{(L-1)}_{ji}$, $a^{(L)}_j = g(z^{(L)}_j)$, 换一下

令$f(z) =-\frac 1 m \sum_{k=1}^K \sum_{i=1}^m y_k^{(i)} ln(g(z)) + (1-y_k^{(i)}) ln(1 - g(z))$

求导得$\frac{df}{dz} =-\frac 1 m \sum_{k=1}^K \sum_{i=1}^m y_k^{(i)} \frac{g'(z)}{g(z)} + (1-y_k^{(i)}) \frac{-g'(z)}{1-g(z)}$

利用sigmoid函数性质, 推得$\frac {df}{dz} = g(z)_k - y_k^{(i)} = a^{(L)}_k - y_k^{(i)}$

现在我们要求所有$\theta^{(l)}_{ji}$的偏导，即$\frac{\partial f}{\partial \theta} = \frac{df}{dz} \frac{\partial z}{\partial \theta}$

举个简单得例子，考虑神经网络得得正向路径a->b->c->d

$z^{(L)}_d = \theta^{(L-1)}_{dc} a^{(L-1)}_c = \theta^{(L-1)}_{dc} g(\theta^{(L-2)}_{cb} a^{(L-2)}_b)= \theta^{(L-1)}_{dc} g[\theta^{(L-2)}_{cb} g(\theta^{(L-3)}_{ba} a^{(L-3)}_a)]$

$\frac{\partial z}{\partial \theta^{(L-3)}_{ba}} = \theta^{(L-1)}_{dc} g'(z^{(L-1)}_c) \theta^{(L-2)}_{cb} g'(z^{(L-2)}_b) a^{(L-3)}_a$ （注意g里面是z别和a搞混了）

前面系数两两一组，每组第一个是从后一层转移，第二个是乘当前层系数

最后单独剩一个系数

考虑线性性，所有像例子中这样的路径叠加就是结果

首先我们对于每组数据$(x^{(i)}, y^{(i)})$，进行FP，得到每一层的激活值。

然后我们进行BP，得到每个theta在这组数据下的J的偏导

先考虑两两一组的系数，我们记$\delta^{(l)}_i$记录第$l$层第$i$个非bias unit的后续系数和

那么$\delta^{(L)}_k = a^{(L)}_k -y_k^{(i)} $

转移：$\delta^{(l)} = (\theta^{(l)})^T \delta^{(l+1)}$

乘当前层：$\delta^{(l)}$.*$g'(z^{(l)})$ ，其中由sigmoid性质得 $g'(z^{(l)}) = a^{(l)}$.*$(1 - a^{(l)})$

剩下的单独那个系数就好办了。

$\Delta^{(l)}_{ji} = \delta^{(l+1)}_j a^{(l)}_i$。这居然也可以矩阵化: $\Delta^{(l)} = \delta^{(l+1)} (a^{(l)})^T$ （竖的乘横的）

最后补上regularization那项就好了，注意$i=0$得$\Delta$不用补